En mécanique un levier est une pièce rigide, allongée, généralement en liaison pivot ou en simple appui par rapport à une partie fixe, qui permet de transformer un mouvement. Le levier est l'une des huit machines simples.
Le levier peut être utilisé de deux manières :
• pour amplifier un mouvement, en amplitude ou en vitesse ; l'une des premières applications fut sans doute l'atlatl ;
• pour amplifier un effort.
Les deux utilisations sont contradictoires : l'amplification du mouvement se fait aux dépens de l'effort, et l'amplification de l'effort se fait aux dépens de la vitesse et de l'amplitude du mouvement.
Pour que le levier puisse jouer, il doit avoir un appui, appelé également hypomochlion ou hypomoclion (du grec ὑπο « sous » et μοχλός « levier »). C’est aussi l’axe sur lequel on peut faire levier pour tourner. Ce terme est utilisé, notamment en odonto-stomatologie, pour désigner le centre de rotation de la dent par rapport à son ancrage, au niveau du desmodonte.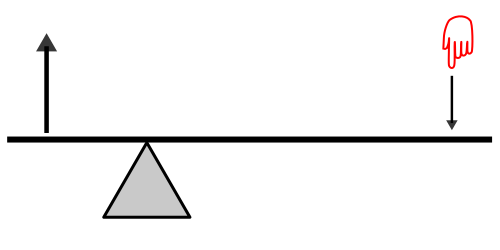
Le bras de levier est la distance séparant une extrémité du levier de son point d’appui. C'est aussi le rapport des deux bras, qui donne l'amplitude de l'effet de levier.
Pi(π)
Pi(π) , appelé parfois constante d’Archimède , est un nombre représenté par la lettre grecque minuscule du même nom : π. C’est le rapport constant de la circonférence d’un cercle à son diamètre dans un plan euclidien. On peut également le définir comme le rapport de la superficie d’un cercle au carré de son rayon.
Sa valeur approchée par défaut à moins de 0,5×10–15 prèsb est 3,141 592 653 589 793 en écriture décimale.
De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques.
Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. C’est même un nombre transcendant, ce qui signifie qu’il n’existe pas de polynôme non nul à coefficients entiers dont π soit une racine.
La détermination d’une valeur approchée suffisamment précise de π, et la compréhension de sa nature sont des enjeux qui ont traversé l’histoire des mathématiques ; la fascination exercée par ce nombre l’a même fait entrer dans la culture populaire.
L’usage de la lettre grecque π, première lettre de « περίμετρος » — périmètre en grec —, n’est apparu qu’au XVIIIe siècle. Auparavant, sa valeur était désignée par diverses périphrases comme la « constante du cercle » ou son équivalent dans diverses langues.
Archimède a inventé, vers 250 avant J-C, une méthode originale pour le calcul de la longueur d'un cercle. Il encadre en effet cette valeur par le périmètre d'un polygone régulier inscrit dans ce cercle, et par le périmètre d'un polygone régulier exinscrit :
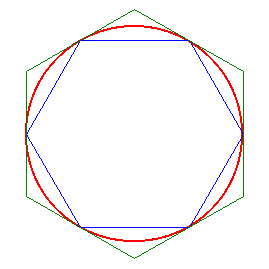
Le périmètre du cercle est compris est entre le périmètre de l'hexagone bleu et celui de l'hexagone en vert .
Cette méthode préfigure le calcul intégral de Newton et Leibniz, près de 2000 ans avant son invention effective. En utilisant un polygone à 96 côtés, Archimède parvient à l'excellente approximation :
Poussée d'Archimède
Tout corps plongé dans un fluide (liquide ou gaz) a un poids apparent plus faible que son poids réel G, c'est-à-dire la force exercée par notre planète sur ce corps.
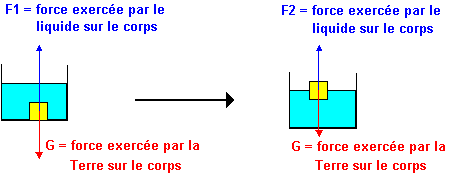
La force F1, lorsque ce corps est immergé, a une intensité plus élevée que la force G exercée sur le corps par la Terre: il monte jusqu'au moment où ces deux forces ont la même intensité, elles s'annulent (F2 = G) et le corps flotte. Notez que la force G peut avoir une intensité plus élevée que F1, le corps ne monte pas, il a seulement un poids apparent plus faible que son poids réel G.
Il existe donc une force exercée par le fluide qui pousse ce corps vers le haut, c'est cette force qui est appelée poussée d'Archimède et est notée F(a) (une poussée est une force, pas une pression).
Si le poids du corps est noté G et si son poids apparent est noté G(app), nous avons la formule:
G(app) = G - F(a) ou F(a)= G -G(app)
Si le corps flotte ou est en équilibre dans un fluide, son poids apparent G(app) est nul et nous obtenons la formule:
Corps flottant: F(a) = G
• La poussée d'Archimède varie en fonction du volume immergé V(i) du corps, de la masse volumique ρ du fluide.
• La poussée d'Archimède ne varie pas avec la profondeur h d'immersion lorsque le corps est totalement immergé, ce qui est étonnant (la pression n'est donc pas un facteur significatif de la poussée d'Archimède).
La principe d'Archimède dans l'air
Selon le principe d'Archimède, tout corps plongé dans un fluide (liquide ou gaz) subit une poussée verticale, de bas en haut, égale au poids du volume de fluide déplacé.Un corps, libre de se déplacer dans l'atmosphère, et d'une densité inférieure à celle de l'air, décolle. C'est le domaine des ballons.
Il y a deux moyens d'obtenir cette faible densité :
• En chauffant l'air contenu dans une enveloppe (ouverte à la base). Ce sont les montgolfières
• En remplissant une enveloppe fermée par un gaz plus léger que l'air (l'hydrogène « très inflammable »,l'hélium).
Les objets volants comme les avions et les planeurs soumis à une poussée d’Archimède négligeable par rapport à leur poids puisqu’ils sont beaucoup plus lourds que l’air. La force qui leur permet de s’envoler, puis de voler à une altitude fixée, que l’on appelle la portance , est encore la résultante des forces de pression sur leur périphérie. La nouveauté tient d’abord à la vitesse de ces objets : les avions à l’arrêt sur les aéroports ne peuvent pas s’envoler, ils ne parviennent à décoller qu’en roulant et après avoir dépassé une certaine vitesse.
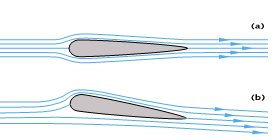
Pour comprendre l’origine de cette portance, plaçons-nous d’abord dans un cas simplifié à l’extrême, en imaginant une aile mince, symétrique, et d’envergure infinie. Le vol de cette aile à une vitesse V devient un phénomène à deux dimensions, illustré sur la Figure a. Imaginons un observateur solidaire de cette aile, qui, comme le passager d’un avion, voit le fluide extérieur venir de l’amont avec la vitesse V. Dans le cas où l’aile vole avec une incidence nulle, l’écoulement au-dessus de l’aile, ou le long de l’extrados , et l’écoulement au-dessous de l’aile, ou le long de l’intrados , sont identiques. Les pressions sur l’intrados et l’extrados sont aussi symétriques et la composante verticale de leur résultante ne peut être que nulle, cette aile n’est soumise à aucune portance.
Pour plus d'explication voir la vidéo
Vis d'Archimède
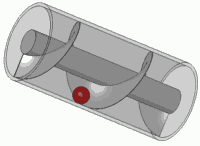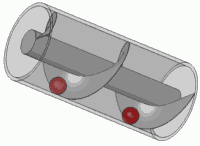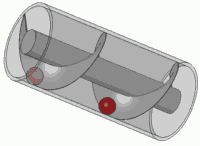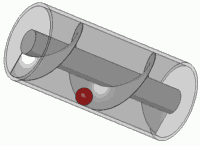La vis d'Archimède , parfois aussi nommée escargot, voire abusivement appelée vis sans fin ,est un dispositif qu'Archimède aurait mis au point lors d'un voyage en Égypte, permettant aux habitants du bord du Nild'arroser leurs terrains. La tradition d'attribuer cette invention à Archimède peut seulement refléter que ce dispositif était inconnu des Grecs à l'époque hellénistique et qu'il a été introduit au IIIe siècle av. J.-C. par des ingénieurs grecs non connus, bien que certains auteurs ont suggéré qu'il était déjà en usage en Assyrie 350 ans avant, notamment pour alimenter en eau les jardins suspendus de Babylone. Léonard de Vinci s'en est inspiré pour sa vis aérienne.
Pi(π) , appelé parfois constante d’Archimède , est un nombre représenté par la lettre grecque minuscule du même nom : π. C’est le rapport constant de la circonférence d’un cercle à son diamètre dans un plan euclidien. On peut également le définir comme le rapport de la superficie d’un cercle au carré de son rayon.
Sa valeur approchée par défaut à moins de 0,5×10–15 prèsb est 3,141 592 653 589 793 en écriture décimale.
De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques.
Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. C’est même un nombre transcendant, ce qui signifie qu’il n’existe pas de polynôme non nul à coefficients entiers dont π soit une racine.La détermination d’une valeur approchée suffisamment précise de π, et la compréhension de sa nature sont des enjeux qui ont traversé l’histoire des mathématiques ; la fascination exercée par ce nombre l’a même fait entrer dans la culture populaire.
L’usage de la lettre grecque π, première lettre de « περίμετρος » — périmètre en grec —, n’est apparu qu’au XVIIIe siècle. Auparavant, sa valeur était désignée par diverses périphrases comme la « constante du cercle » ou son équivalent dans diverses langues.
Archimède a inventé, vers 250 avant J-C, une méthode originale pour le calcul de la longueur d'un cercle. Il encadre en effet cette valeur par le périmètre d'un polygone régulier inscrit dans ce cercle, et par le périmètre d'un polygone régulier exinscrit :
Le périmètre du cercle est compris est entre le périmètre de l'hexagone bleu et celui de l'hexagone en vert .
Cette méthode préfigure le calcul intégral de Newton et Leibniz, près de 2000 ans avant son invention effective. En utilisant un polygone à 96 côtés, Archimède parvient à l'excellente approximation :
Poussée d'Archimède
Tout corps plongé dans un fluide (liquide ou gaz) a un poids apparent plus faible que son poids réel G, c'est-à-dire la force exercée par notre planète sur ce corps.
La force F1, lorsque ce corps est immergé, a une intensité plus élevée que la force G exercée sur le corps par la Terre: il monte jusqu'au moment où ces deux forces ont la même intensité, elles s'annulent (F2 = G) et le corps flotte. Notez que la force G peut avoir une intensité plus élevée que F1, le corps ne monte pas, il a seulement un poids apparent plus faible que son poids réel G.
Il existe donc une force exercée par le fluide qui pousse ce corps vers le haut, c'est cette force qui est appelée poussée d'Archimède et est notée F(a) (une poussée est une force, pas une pression).
Si le poids du corps est noté G et si son poids apparent est noté G(app), nous avons la formule:
G(app) = G - F(a) ou F(a)= G -G(app)Si le corps flotte ou est en équilibre dans un fluide, son poids apparent G(app) est nul et nous obtenons la formule:
Corps flottant: F(a) = G• La poussée d'Archimède varie en fonction du volume immergé V(i) du corps, de la masse volumique ρ du fluide.
• La poussée d'Archimède ne varie pas avec la profondeur h d'immersion lorsque le corps est totalement immergé, ce qui est étonnant (la pression n'est donc pas un facteur significatif de la poussée d'Archimède).
La principe d'Archimède dans l'air
Selon le principe d'Archimède, tout corps plongé dans un fluide (liquide ou gaz) subit une poussée verticale, de bas en haut, égale au poids du volume de fluide déplacé.Un corps, libre de se déplacer dans l'atmosphère, et d'une densité inférieure à celle de l'air, décolle. C'est le domaine des ballons.
Il y a deux moyens d'obtenir cette faible densité :
• En chauffant l'air contenu dans une enveloppe (ouverte à la base). Ce sont les montgolfières
• En remplissant une enveloppe fermée par un gaz plus léger que l'air (l'hydrogène « très inflammable »,l'hélium).
Les objets volants comme les avions et les planeurs soumis à une poussée d’Archimède négligeable par rapport à leur poids puisqu’ils sont beaucoup plus lourds que l’air. La force qui leur permet de s’envoler, puis de voler à une altitude fixée, que l’on appelle la portance , est encore la résultante des forces de pression sur leur périphérie. La nouveauté tient d’abord à la vitesse de ces objets : les avions à l’arrêt sur les aéroports ne peuvent pas s’envoler, ils ne parviennent à décoller qu’en roulant et après avoir dépassé une certaine vitesse.
Pour comprendre l’origine de cette portance, plaçons-nous d’abord dans un cas simplifié à l’extrême, en imaginant une aile mince, symétrique, et d’envergure infinie. Le vol de cette aile à une vitesse V devient un phénomène à deux dimensions, illustré sur la Figure a. Imaginons un observateur solidaire de cette aile, qui, comme le passager d’un avion, voit le fluide extérieur venir de l’amont avec la vitesse V. Dans le cas où l’aile vole avec une incidence nulle, l’écoulement au-dessus de l’aile, ou le long de l’extrados , et l’écoulement au-dessous de l’aile, ou le long de l’intrados , sont identiques. Les pressions sur l’intrados et l’extrados sont aussi symétriques et la composante verticale de leur résultante ne peut être que nulle, cette aile n’est soumise à aucune portance.
Pour plus d'explication voir la vidéo
Vis d'Archimède